Repro toybox

1. In order to correct perspective deformations, some markers are put onto the same plane the target object resides on. Usually, images of randomly distributed squares are used as markers. Also, the markers have to be present in digital form, accessible by the program. Then, features (e.g. SURF) can be detected in both the marker images and the recorded image (also containing the marker). The features in the recorded image can be matched in a naive nearest-neighbour fashion against each marker image (independently). From the resulting correspondences, the homography can be computed and thus the image can be projected into a relatively exact top-down view - like the camera would have been exactly vertical above the object.
   
   Additionally, one may want to correct colours, as they may have been distorted by the imaging procedure. For this, again a reference is placed on the ground, such that it is also visible in each image. The reference image shows some colours in an ordered manner, such that they can be found in the geometrically corrected image. In my test situations, the colour reference was an image that contained some squares of the same colour, arranged in a rectangle. If again the true colours are known, they can be compared to the measured ones. A low degree polynomial can then be fitted in order to find the transformation used for colour correction.
   
   In order to give some qualitative measurements even for uncalibrated cameras, the layout has to be digitally available. Then, distances can be measured which allows a more flexible approach to further refinement steps (such as cropping).
   
   In short, one does the following:
   • Take a picture of the prepared scene, containing the target object, markers and colour reference.
   • Detect features in all marker images and the taken picture.
   • Match the features of the taken picture against all marker images.
   • Compute the homography between the virtual layout and the input image.
   • Transform the input image.
   • Find the colour reference, identify the individual colour measurements.
   • Using the (exact) colour reference and the colour measurements, fit a polynomial.
   • Correct colours in the source image.
   • Apply other image alterations.
   
   
2. The second problem is much more involved. It's assumed that the object type is known (e.g. a book) and the profile can be measured. Then, a (possibly non-linear) function can be fitted through the profile data points. This function can be used to compute the location of a real point (on the surface of the book) in the image and thus generate an image in which the page appears flat.
   
   The main issue with this approach is that the shape of a bended page has to be formalized and a procedure to fit a possibly non-linear function is required. The second issue can be handled by using a non-linear least squares algorithm (Gauss-Newton or Levenberg-Marquardt). The target function has to be found manually.
   
   The profile can be extracted using various approaches. The simples one is to place a camera such that the profile is captures. With some (simple and hopefully automatable) postprosessing steps, the profile can be extracted relatively easy. Other approaches, such as stereo matching, are more complex but probably more comfortable
   
   Using the simple profile-capturing technique and a pair of independently fitted exponential functions, one can retrieve the shape of the profile. As an example, an experimental result of this process is shown below:
   
   
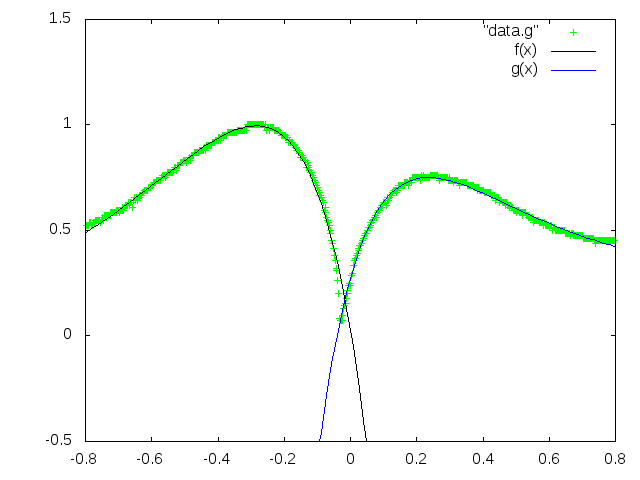
   So far, this is merely a proof-of-concept, which depends on some manual preprocessing. None the less, the results of this simple approach are quite impressive and remaining issues should be manageable.