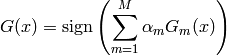4.3.5. Boosting¶
4.3.5.1. AdaBoost¶
Given 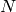 training data points and
training data points and 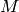 classifiers. The AdaBoost algorithm does the following:
classifiers. The AdaBoost algorithm does the following:
Initialize weights
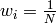
For
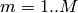 :
:- Fit the classifier
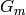 to the training data using weights
to the training data using weights 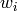
- Compute the classifier error
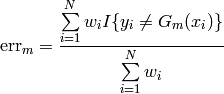
- Compute the classifier weight
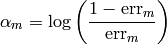
- Recompute all data weights
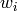
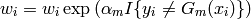
- Fit the classifier
The combined classifier is
4.3.5.2. Interfaces¶
- class ailib.fitting.AdaBoost¶
Bases: ailib.fitting.model.Model
AdaBoost algorithm.
Given M (weak) classifiers, AdaBoost iteratively trains each one of them with respect to so far misclassified samples. For a formal representation, consult the respective documentation.
As can be seen from the schematics, the classifiers are required to support weighted samples. The classifiers have to be linked to the instance of this class before training. This can be achieved through calls to the AdaBoost.addModel() method.
- addModel(m)¶
Add a trainable model to the set of boosted classifiers.
The models are required to support weighted samples.
Parameter: m (Model) – Model
- err((x, y))¶
- Return the distance between the target y and the model prediction at the point x.
- eval(x)¶
Evaluate the model at data point x.
The outcome is the majority vote over the outcome of all classifiers w.r.t. their weight (note the formal representation).
- fit(data)¶
Apply the AdaBoost algorithm on the presented data set.
Parameter: data – Training data. Returns: self