4.3.6. Trees and Random Forests

Contents

• Trees and Random Forests
  • Decision tree
  • Random forest
  • Interfaces
    • Classification
    • Regression
  • Examples

4.3.6.1. Decision tree

The tree growing algorithm can be sketched as follows:

1. Grow the tree

   1. Given the data, determine the optimal dimension j and splitting point s.

      

   where 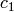and 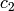are the labels of the (hypothetical) leaves.

   2. Grow two child trees on the respective data subsets.
   3. Stop, if the number of data points is below some threshold.

2. Prune the tree

   1. Collapse the internal node that produces the smallest per-node increase in the tree cost.
   2. Stop, if there’s only one node left (the root).
   3. Out of the produced sequence of trees, select the one that minimizes the total tree cost.

Stumps are single-node trees with the node labels fixed to 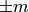. Also for stumps, the learning consists of finding the optimal splitting dimension 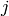and threshold . Because stumps are classifiers, the 0-1 loss function is used as error measurement. Thus, each stump has to solve the optimization problem:

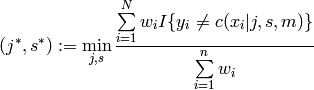
Additionally to the training input, each training sample 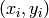is assigned a weight 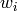that represents how much a misclassification of the sample contributes to the classifier cost.

4.3.6.2. Random forest

4.3.6.3. Interfaces

class ailib.fitting.Tree(leafThres=5)

Bases: ailib.fitting.model.Model

Decision tree skeleton.

Warning

Don’t use this class directly. Use RegressionTree or ClassificationTree instead.

Parameter:leafThres (int) – Minimum number of data points per node.

cleanData()

Remove the data from the tree.

Only the data member is cleared. The node label is recomputed first.

collude()

Collapses the childs of the node.

The childs’ data is collected in this node and the label recomputed. The childs will be deleted. The node will become a leaf.

costSplit(j, s)

costTerminal(data)

costTree(alpha)

data()

Return the data of all child nodes.

depth()

Return the maximal depth of the tree.

eval(x)

Find the label of a data point x.

grow(data)

Grow a tree on training data.

Finds the optimal splitting parameters of the data and grows two child trees (if there are enough data points left).

Parameter:data (STD) – Training data.

isLeaf()

Return true, if the node has no childs (is a leaf node).

leaves()

Return the number of leaves.

prune(alpha)

Prune the tree to find the tree with minimal cost.

The tree is pruned according to weakest link pruning until there’s only one node left. Then, the tree with minimal total cost is restored.

Parameter:alpha (float) – Pruning parameter. Controls, how much the tree size influences its cost.

class ailib.fitting.Stump(labelValue=1.0)

Bases: ailib.fitting.model.Model

Parameter:labelValue (float) – Label of the class.

err((x, y))

0-1 loss function.

eval(x)

Compute the label of a data point x.

fit(data, weights=None)

Train the stump on the presented data.

Finds the optimal dimension and splitting point to split the data in two subsets. The optimal parameters are found w.r.t. to the data weights. If no weights are given, a uniform distribution is assumed.

Parameters:

• data (STD) – Data points.
• weights ([float]) – Weights of data points. Needs not to be normalized.

4.3.6.3.1. Classification

class ailib.fitting.ClassificationTree(alpha=0.0, leafThres=5)

Bases: ailib.fitting.tree.Tree

Parameters:

• alpha (float) –
• leafThres (int) –

costSplit(data, j, s)

costTerminal(data)

costTree(alpha)

err((x, y))

fit(data)

4.3.6.3.2. Regression

class ailib.fitting.RegressionTree(alpha=0.0, leafThres=5)

Bases: ailib.fitting.tree.Tree

Parameters:

• alpha (float) –
• leafThres (int) –

costSplit(data, j, s)

costTerminal(data)

costTree(alpha)

err((x, y))

fit(data)

4.3.6.4. Examples