6. Glossary¶
- 0-1 loss function
The cost of a missclassification is one, the cost of a correct classification zero.:
if label == prediction: cost = 0.0 else: cost = 1.0
In mathematical formulations, this can also be written as:
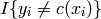
- Bootstrapped
- see Bootstrapping
- Bootstrapping
- Given N samples, the bootstrapped dataset contains N points randomly drawn with replacement from the original dataset.
- Classification
- In classification problems, an input feature has to be assigned to a certain class. Often, classes represent some attributes or characteristics of the possible input, i.e. divide the input space in discrete regions. Classification can also be seen as a coding scheme, where an input string has to be assigned to one codebook entry.
- Data point
- Training data point, usually represented as a feature.
- Expectation-Maximization
- This term refers to an iterative algorithm scheme, consisting of two steps. It is applied in maximum likelihood methods, where some information is missing (hidden). In the E-step, the hidden states are estimated according to the currently computed model. Then, the model is again recomputed using the estimated hidden states in the M-step. These two steps are repeated, until the procedure converged.
- Feature
- Description of a data point. Represented by a vector [
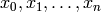] - Generalization error
- The generalization error expresses how well a trained model behaves on any possible (so far not seen) input. Loosely speaking, it shows how well the model represents the true underlying problem. In general, it cannot be measured nor computed, at most estimated.
- Gradient
Given a function
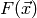with 
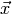being a vector of variables 
.
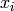Then, the gradient is the vector of all first order partial derivatives w.r.t each
component of 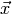:![\nabla(\vec{x}) := \left[ \frac{\partial F }{ \partial x_0 }(\vec{x}), \frac{\partial F }{ \partial x_1 }(\vec{x}),
\dots, \frac{\partial F }{ \partial x_n }(\vec{x}) \right]^T](_images/math/c6afe3d05fdb402dbe1fd705478e8863861f1cf6.png)
- Hessian matrix
![H(\vec{x}) = \left[ \frac{ \partial^2 f }{ \partial x_i \partial x_j }(\vec{x}) \right]_{ij}](_images/math/4159d3e63aaa9398e94f291ee19aca98cd67b1f7.png)
- i.i.d
- Identically, independent distributed
- Jacobian matrix
Given a function with parameters
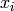and input values 
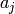. The Jacobian matrix holds
the first order partial derivative w.r.t every parameter, evaluated at each input value:![\mathbf{J}(a)_{ij} = \left[ \, \frac{\partial f }{ \partial x_i}(a_j) \, \right] = \begin{pmatrix}
\frac{ \partial f(a_0) }{ \partial x_0 } & \frac{ \partial f(a_0) }{ \partial x_1 } & \dots & \frac{ \partial f(a_0) }{ \partial x_M } \\
\frac{ \partial f(a_1) }{ \partial x_0 } & \frac{ \partial f(a_1) }{ \partial x_1 } & \dots & \frac{ \partial f(a_1) }{ \partial x_M } \\
\dots & & & \\
\frac{ \partial f(a_N) }{ \partial x_0 } & \frac{ \partial f(a_N) }{ \partial x_1 } & \dots & \frac{ \partial f(a_N) }{ \partial x_M }
\end{pmatrix}](_images/math/60faea0a6ab5c2a22338dd747bb6b9928f11b24d.png)
- Label
- In supervised learning situations, the label specifies the optimal model outcome. In classification problems, the label is a class identifier, in regression problems it’s the target value (in the function’s range).
- Maximum likelihood
- Given a model with some - so far unspecified - parameters, the maximum likelihood estimation denotes a method to determine the parameters optimally, given training data.
- Model
- The core of each learning problem is the model. Given some training data and a learning goal, the model is a mathematical representation that captures the shape or structure of the underlying problem. The model can usually be trained, i.e. fitted to the training data, and produce an output that can be mapped to the learning goal.
- Overfitting
In many learning problems, one desires to come up with a model that minimizes the prediction error on a training set. Unfortunately, models with higher complexity often decrease the training error but rely too much on the concrete data set.
As an example, consider polynomial fitting. A high order polynomial fits any training set well but also includes all noise from the data in the model. If the data (say 100 data points) is noisily distributed along a parabola, a polynom of high order (e.g. 100) will give a low training error but isn’t capable of capturing the actually relevant information (the shape of the parabola).
The term overfitting describes a situation where the complexity of the chosen model does not match the complexity of the actual underlying problem, resulting in a trained model that only works for the training data. In general, such situations cannot be detected automatically (as the training error is actually minimal). Typically the testing error will be very low while the generalization error is high.
- Regression
- Regression problems deal with adapting a continous function to measured training data. Often, the target function given in a general form, including parameters. The goal of regression is to determine parameter values, such that the training data is optimally represented by the function.
- STD
- Supervised training data: [(feature, label)]
- Testing error
- The training error identifies the error statistics of a trained model over all data points in the testing set. Usually, the testing set is a subset of the originally measured data, not used for training. As the testing set is limited, the testing error cannot be equal to the generalization error. Yet, it is used to give a hint how well the trained model will behave on new data.
- Testing set
- In order to measure the testing error, a set of data is needed that was not already seen by the model, i.e. not used to train (fit) the model. Hence, the part of available data which is reserved for this task is called the testing set. Testing data is only available in the case of supervised learning (yet, there may be exceptions). The format is determined by STD.
- Training error
- The training error identifies the error statistics of a trained model over all data points in the training set.
- Training set
- The testing set is the collection of data which is used to train (fit) a model. For supervised learning, the training set is a list of tuples (the feature and label). In the case of unsupervised learning, the training set is simply the list of features. (See also STD and UTD).
- UTD
- Unsupervised training data: [feature]