5. selection — Model selection and validation¶
Contents
5.1. Information Criteria¶
In maximum likelihood methods, the Bayesian and Akaike information criteria give a measurement
Let 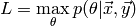 be the likelihood of the most probable
model parameters
be the likelihood of the most probable
model parameters 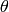 with respect to the training data
with respect to the training data 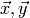 .
Furthermore, let the model have
.
Furthermore, let the model have 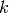 free parameters that are estimated and let there
be
free parameters that are estimated and let there
be 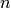 training samples. The two information criteria are defined in the following way:
training samples. The two information criteria are defined in the following way:
Bayesian information criterion
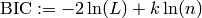
Akaike information criterion
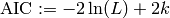
From this definition, it can be seen that the criteria add a complexity penalty to the parameter likelihood. The reason behind this is the following: it’s assumed that the higher the number of parameters, the better any set of training data can be approximated by the model. For example, consider polynomial fitting. The number of free parameters corresponds to the order of the fitted polynomial. Given a degree equal to the number of training samples, the polynomial can be fitted perfectly. But as it will be a curve through all given data pairs, the generalization power will be poor. The goal is to find a model with reasonable number of parameters but at the same time a low training error (i.e. a high maximum likelihood).
If the error is normal i.i.d with variance 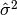 , the criteria can be stated as:
, the criteria can be stated as:
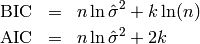
Instead of the Akaike information criterion, one should rather empoly the corrected AIC:
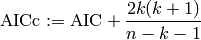
As 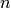 gets large, the two criteria are identical. If
gets large, the two criteria are identical. If 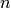 is relatively small, the original
AIC may suggest models with a larger number of parameters, thus is more likely to be subject of overfitting.
is relatively small, the original
AIC may suggest models with a larger number of parameters, thus is more likely to be subject of overfitting.
5.2. K-Fold Cross-Validation¶
The cross-validation method tries to estimate the generalization error of a model, given some training data.
For 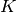 -fold cross-validation, the
-fold cross-validation, the 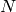 samples are split into
samples are split into 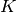 subsets of equal size. Then,
subsets of equal size. Then, 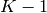 subsets are used as training set and the remaining subset as testing set:
subsets are used as training set and the remaining subset as testing set:
Split the data into
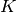 subsets.
subsets.For
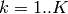
- Fit the model using all subsets except the
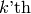 .
. - Compute the testing error
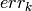 on the
on the 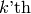 subset.
subset.
- Fit the model using all subsets except the
The estimated generalization error is the average of the errors of the
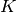 testing sets.
testing sets.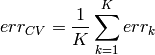
If 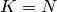 , each sample is once used as testing set (consisting of only this sample).
This special case is called Leave-one-out cross-validation.
, each sample is once used as testing set (consisting of only this sample).
This special case is called Leave-one-out cross-validation.
5.3. Random Sample Consensus¶
Given a set of training data that is noisy and contains outliers, i.e. erroneous data. The aim of the RANSAC algorithm is to determine which data points are outliers and compute the model without those.
Given the minimal number of points 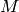 required to fit the model and a threshold, the
algorithm does the following:
required to fit the model and a threshold, the
algorithm does the following:
Iterate until convergence
- Out of all data points, select
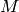 points randomly (the root set).
points randomly (the root set). - Fit the model to these.
- Compute the prediction error for all data points.
- Add all points for which the error is below a threshold to the consensus set of this iteration.
- Out of all data points, select
Fit the model using all points in the largest consensus set.
As convergence criterion, the probability that at least one outlier free root set was chosen can be tracked.
Let  be the number of iterations and
be the number of iterations and  the ratio of inliers and outliers.
the ratio of inliers and outliers.
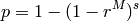
Because  is not known beforehand, it is estimated by
is not known beforehand, it is estimated by 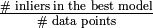 .
The algorithm iterates, until
.
The algorithm iterates, until 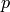 exceeds some value (usually close to one, e.g.
exceeds some value (usually close to one, e.g. 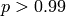 ).
).
5.4. Interfaces¶
- ailib.selection.crossValidation(data, model, K)¶
Parameters: - data (STD) – Data points.
- model (ailib.fitting.Model) – Model to fit the data points to.
- K (int) – Number of buckets.
Returns: Cross-validation error.
- class ailib.selection.Ransac(thres, minPts, prob=0.98999999999999999, maxIter=100)¶
Parameters: - thres (float) – Error threshold.
- prob (float) – Minimum probability of finding an outlier-free root set.
- maxIter (int) – Maximum number of iterations.
- minPts (int) – Minimum number of points the model requires to be computed.
- fit(data, model)¶
Parameters: - data (STD) – Training data.
- model (ailib.fitting.Model) – Model to be fit.
Returns: model instance, fitted to the optimal consensus set.