4.3.3. k-Nearest Neighbour

Contents

• k-Nearest Neighbour
  • Interfaces
  • Examples

The idea of k-Nearest neighbour classification very simple. First some training data has to be provided. Then, any new data point is assigned the same label as the majority of its k closest training data points. In the simplest case, this looks like this:

1. Store all training points

2. When a new data point is presented, compute the distance to all training points. As default, the euclidean distance is used, i.e.

   

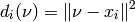
3. Select the training samples with k smallest distances.

4. Return the label of the selected training samples that appeared most often.

If sample weights are given, the distance in the second step is modified:

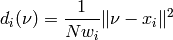
This adjustment makes it more probable for a sample with a large weight to be in the set of nearest neighbours. Instead of a majority vote on the labels, it is also possible to pick a label at random (with respect to the distance to that point).

Only the base algorithm is implemented here. If a more advanced implementation is required, have a loot at the scikit-learn package.

4.3.3.1. Interfaces

class ailib.fitting.kNN(k, dist=<function <lambda> at 0x36ec140>)

Bases: ailib.fitting.model.Model

k-Nearest Neighbour matching.

A data point x is assigned to the same class as the most of its k nearest neighbours.

if weights are given, the distance will be computed as

>>> 1.0/(N*weight[i]) * dist(data[i],x)

There are three evaluation types:

• The most often appeared label (majority vote, the default).
• Sampled from all neighbours with uniform probability (mixin Sampling).
• Sampled from all neighbours with respect to their distances (mixin WeightedSampling).

The distance measurements

• distAbs: absolute distance .
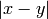• distNorm: norm .
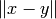• distSqNorm: squared norm .

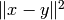are made available. Change the distance function by assignment to obj.dist For the lower ones, the data should be passed as list or a scipy.matrix. The default is distSqNorm.

Parameters:

• k (int) – Parameter which specifies the size of the neighbourhood.
• dist ((Num b) => a -> a -> b) – Distance measurement on data points.

class Sampling

Mixin for sampling with uniform probabilities.

eval(x)

Samples the label from all k nearest neighbours.

All neighbours are equally likely to be drawn.

class kNN.WeightedSampling

Mixin for sampling with respect to distances.

eval(x)

Samples the label from all k nearest neighbours with respect to their distance.

The sampling weights are inverse proportional to the distance:

>>> w[i] = 1.0/(dist(data[i],x))

with weights enabled

>>> w[i] = N * weights[i] / dist(data[i], x)

kNN.err((x, y))

0-1 loss function.

kNN.eval(x)

Return the label of the most frequent class of the k nearest neighbours of x.

If there are two classes with the same number of occurrences in the k-neighbourhood of x, one of them is chosen at random (i.e. ties are broken randomly).

kNN.fit(data, labels, weights=None)

Set up the data points for later matching.

4.3.3.2. Examples