4.3.7. Clustering¶
Contents
4.3.7.1. K-Means¶
The K-Means algorithm is used for clustering of unsupervised data.
Classically, the algorithm is sketches as follows:
- Initialize cluster centers at randomly chosen data points.
- Iterate until convergence
- Assign each data point to the closest cluster (E-Step).
- Recompute the cluster centers as the average of all associated data points (M-Step).
- A new data point is classified according to the closest cluster center.
As also hinted by the above description, the K-Means algorithm is an instance of an Expectation-Maximization algorithm. The problem can be formalized as
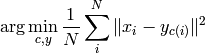
where 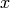 are the data points,
are the data points, 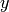 the cluster centers and
the cluster centers and 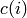 an assignment
function that stores the cluster index for each sample. Setting the derivative w.r.t. the cluster
centers to zero yields the recomputation (M) step. This is the stationary condition, so assignments
are fixed. In the E-Step, the opposite is the case: the assignments are optimized while the
center positions are constant. This yields the optimization problem
an assignment
function that stores the cluster index for each sample. Setting the derivative w.r.t. the cluster
centers to zero yields the recomputation (M) step. This is the stationary condition, so assignments
are fixed. In the E-Step, the opposite is the case: the assignments are optimized while the
center positions are constant. This yields the optimization problem
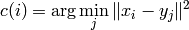
Obviously, the solution is to assign a data point to the closest cluster is the E-Step from the algorithm.
In this library, instead of hard assignments like in the above algorithm, the data can be assigned to the clusters in a probabilistic way. The algorithm then becomes:
Initialize assignment probability matrix:
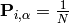 .
.Iterate until convergence
Compute the assignment probabilities (E-Step):
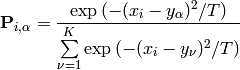
Recompute the cluster centers (M-Step):
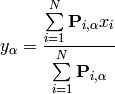
For a new data point
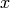 , compute the assignment probabilities
, compute the assignment probabilities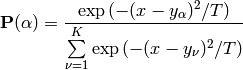
and sample from the discrete distribution formed by
![\{ \mathbf{P}(\alpha) \, | \, \alpha \in [1,K] \}](_images/math/86a914d5f1faf04bb17eba62b5e7d93f5c803f95.png) .
.
The matrix 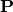 stores the assignment probabilities to all clusters for each sample. Note
that
stores the assignment probabilities to all clusters for each sample. Note
that 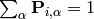 . This representation comes from a maximum entropy approach.
. This representation comes from a maximum entropy approach.
The risk is defined as in the ‘normal’ algorithm. The E-Step assumes fixed cluster centers, so the risk can be expressed as:
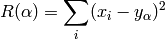
and inserted into the gibbs distribution (which maximizes the entropy) with parameter 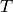 .
.
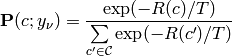
Note that 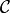 denotes the set of all possible assignments. The equation can be reformulated
to give the probability of an assignment
denotes the set of all possible assignments. The equation can be reformulated
to give the probability of an assignment  (given the cluster centers
(given the cluster centers 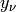 ) and from
there, the assignment probabilities
) and from
there, the assignment probabilities 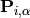 used in the E-Step are found.
Further, the entropy maximization for the cluster center is:
used in the E-Step are found.
Further, the entropy maximization for the cluster center is:
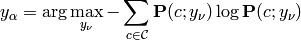
This equation can be again solved using the stationary condition (setting the second derivative w.r.t.
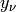 to zero) and gets the M-Step of the algorithm.
to zero) and gets the M-Step of the algorithm.
In this representation, the parameter 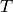 is introduced. A large temperature
is introduced. A large temperature 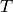 leads to fewer diverse centers and uniform assignment probability of the data to the centers.
A small temperature results in the inverse effect: The centers become distinct and the assignment
probability of each sample tends towards one for one cluster and zero for the others.
Loosely speaking, the temperature controls how strongly the clusters are influenced by the data, i.e
how sensitive the algorithm is to the input data.
leads to fewer diverse centers and uniform assignment probability of the data to the centers.
A small temperature results in the inverse effect: The centers become distinct and the assignment
probability of each sample tends towards one for one cluster and zero for the others.
Loosely speaking, the temperature controls how strongly the clusters are influenced by the data, i.e
how sensitive the algorithm is to the input data.
4.3.7.2. Interfaces¶
- class ailib.fitting.Kmeans(numClusters, tol=1, maxIter=100, temp=1.0, dist=<function <lambda> at 0x36eacf8>)¶
Bases: ailib.fitting.kNN.kNN
K-Means algorithm.
This is an implementation of the probabilistic K-Means algorithm, not the often used Lloyd algorithm. The default evaluation method is to assign the sample to the closest cluster. Instead, the class label can be sampled from the distances, i.e. the closer to a cluster, the more probable this cluster label will be returned. If this behaviour is desired, use the Kmeans.Soft mixin.
There are several convergence criterions:
- Risk is below a threshold (absoluteRisk).
- risk decrease is below a threshold (relativeRisk).
- Stop after a number of iterations (iterCriterion).
- Assignments don’t change (centerCriterion).
Select one of those by assignment to obj._converged.
Parameters: - numClusters (int) – Number of clusters.
- tol (float) – Threshold for the convergence criterion.
- maxIter (int) – Limit to number of iterations.
- temp (float) – Temperature.
- dist (a -> a -> float) – Distance measurement
- class Soft¶
Sample from clusters according to their distances.
- eval(x)¶
- Return the class of x, sampled from the available clusters.
- Kmeans.fit(data, labels=None, weights=None, T=None)¶
Parameters: - data ([a]) – Training data.
- labels (None) – Unused.
- weigths – Unused.
- T – Temperature. If set, overwrites member.
Returns: self